
Durchschnittliche Fehlerzahl beim 4x4 Memory
EinleitungAufruf zur Facharbeit
Was ist die optimale Spielstrategie?
Erläuterungen zum Rechenverfahren
Tabelle mit allen möglichen Spielverläufen und deren Wahrscheinlichkeiten
Grafik
Einleitung
(zurück)Memory gehört, mathematisch betrachtet, zu einer äußerst interessanten Klasse von Ein-Personen-Spielen, denn man kann einerseits gut und schlecht spielen (auch optimal, was immer das heißen mag), es existiert also eine optimale Gewinnstrategie, andererseits ist der Spielverlauf durch das Spielerverhalten nicht eindeutig festgelegt, da er ja vom Glück abhängt (Hat man Glück, kann man auch ein Spiel mit 0 Fehler beenden!). Memory ist also auch ein Glücksspiel. Wegen dieser Interdependenzen zwischen Zufall und Strategie ist eine mathematische Betrachtung des Spiels aüßerst spannend.
Nachdem ich einige Male das Memoryspiel durchgespielt hatte und beobachtet hatte, dass ich zwar einerseits mit immer weniger Fehlern auskomme, diese aber andererseits auch nur sehr selten unter 4 oder 5 liegen, stellte ich mir (im Wesentlichen) zwei Fragen:
- Wie spielt man optimal?
- Wenn man nun weiß, wie man optimal spielt, welche Fehlerstände erlebt man dann, wie oft erlebt man diese und welchen Fehlerstand erlebt man im "langjährigen Mittel"?
Um das Ergebnis vorweg zu nehmen: Auch dann, wenn man Memory (4 x 4) ohne einen Fehler spielt, also zum Beispiel nichts vergisst oder keine unnötigen Karten aufdeckt, kann es schlimmstenfalls passieren, dass man 7 Fehler macht; im besten Fall kann man auch 0 Fehler erreichen. Alles dazwischen ist natürlich auch möglich. Die Häufigkeiten sind in der Wertetabelle unten angegeben. Im Mittel erreicht ein Spieler, der optimal spielt, 4,4 Fehler!
4,4 Fehler ist also die Messlatte, die es zu erreichen gilt! Mal hat man etwas mehr,
mal etwas weniger. Aber (falls Ihr gut spielt) sollten Euere Ergebnisse um die 4,4 pendeln!
Aufruf zur Facharbeit
(zurück)
Die Berechnung des mittleren Fehlers nachzuvollziehen, ist nicht ganz einfach und erfordert Kenntnisse in Kombinatorik. Ich habe sie letztlich durch systematisches Zusammenstellen aller möglichen Spielverläufe eines optimalen Spielers erhalten und diese computerunterstützt ausgezählt.
Nun ist der Rechenweg alles andere als mathematisch elegant; zwar in bestimmter Hinsicht systematisch, aber letztlich mit der Brechstange! Überdies liegt die erforderliche Rechnerleistung auch noch knapp über den mir zur Verfügung stehenden Ressourcen, was zur Folge hatte, dass ich auch das Abzählverfahren nicht einfach (rekursiv) programmieren konnte, sondern das Problem auch noch mühevoll zerlegen und in Spezialfällen vereinfachen musste. Wer Interesse hat, das Verfahren logisch nachzuvollziehen, kann sich ja die Erläuterungen mal anschauen. Die PC-technische Auszählmethode habe ich nicht dokumentiert.
In solchen Fällen läßt einen gewöhnlich die Frage nach einem eleganten, mathematisch nachvollziehbaren Weg, keine Ruhe. Nachdem ich selbst schon einige Zeit mit dem Problem zugebracht und auch Interessierte schon auf das Problem angesetzt habe (ohne Erfolg), steht zumindest fest, dass eine triviale Lösung wohl nicht ins Haus steht (oder?).
Da im Internet sich eine Menge Mathematiker tummeln, hoffe ich nun auf diesem Weg meiner unruhigen Seele Frieden zu verschaffen.
Wer einen eleganten Weg z.B. durch eine handliche Formel, findet, dem ist ein Ehrenplatz auf der Titelseite meiner Homepage für einige Wochen sicher, ebenso eine würdigende Nachricht an alle, an die ich bis dahin auch die Problemstellung gesandt habe!
Möglich, wenn auch suboptimal, wäre auch eine empirische Bestätigung durch ein Programm, das viele Spiele hintereinander (optimal) spielt und die Ergebnisse dokumentiert. Werden einige 1000 Spiele gespielt, müssten die "Erfolge" des Programms genau die statistischen Wahrscheinlichkeiten bestätigen.
Wer allgemeine Programmiersprachen und deren rekursive Programmiertechniken beherrscht, könnte vielleicht auch alle Spielzüge automatisch erzeugen und auswerten (weil diese PSn) sicherlich weniger Rechnerressourcen benötigen, als mein EXCEL-Ansatz.
Das Thema würde sich (für sehr gute Schüler) auch für eine Facharbeit eignen. An dem Ergebnis wäre ich hochinteressiert! Die WEB-Publikation würde ich "sponsern"!
Also los, Sportsfreunde! :-)
Was ist eine optimale Spielstrategie?
(zurück)
Diese Frage ist vergleichsweise trivial zu beantworten, dazu Folgendes:
- Ist ein Zug gerade abgeschlossen, dann liegen vor einem vier unterschiedliche Klassen von
Karten:
- Die offenen, bereits gefundenen Kartenpaare (Typ 1),
- die zugedeckten Karten, die bereits offen waren und damit bekannt sind (sofern sie nicht vergessen wurden), ich kürze deren Anzahl im Folgenden mit B (wie bekannt) ab (Typ 2),
- die noch nicht aufgedeckten Karten, welche zu den B Karten aus Punkt 2 passen (Typ 3), und
- die noch nicht aufgedeckten Karten, deren Partnerkarten ebenfalls noch nicht aufgedeckt waren (Typ 4).
- Jeder Zug besteht aus zwei Schritten (Schritt A und B). Im Schritt A deckt man natürlich
immer ein Paar aus den Karten vom Typ 2 auf, sofern eines dabei ist. Dies ist ein Schritt
ohne jedes Fehlerrisiko und gestaltet nebenbei das Spielfeld übersichtlicher. Man kann sich
natürlich nur dann so verhalten, wenn man die Position einer bereits offenen Karte nicht wieder
vergisst! Verhielt man sich bereits seit Beginn des Spieles so, so kann auch höchstens ein Paar
unter den zugedeckten Karten sein.
Befindet sich allerdings kein Paar unter den Karten vom Typ 2, muss man immer eine der U unbekannten Karten aufdecken!, da man mit jeder unbekannten Karte (egal ob im Schritt A oder im Schritt B) dasselbe Fehlerrisiko eingeht, bei einem Wagnis sofort im Schritt A aber im Misserfolgsfall wenigstens die Chance hat, einen Informationsgewinn durch 2 neue Karten zu erhalten und damit geringere Fehlerrisiken in den nächsten Spielzügen hat. Dies ist der häufigste Fehler, den ich an Spielern beobachte. - Im Schritt B handelt man dann in einfacher Weise in
Abhängigkeit von Schritt A: Ist die Partnerkarte der in A
aufgedeckten Karte bereits bekannt, deckt man natürlich sofort die passende Karte in Schritt B auf,
ist sie nicht bekannt, verhält man sich im Schritt B wie in A und kann nun entweder zufällig
die zur im Schritt A aufgedeckten Karte Passende aufdecken oder wieder eine neue (vom Typ 3 oder 4).
Im ersten Fall hat man ein Paar gefunden. Im zweiten Fall muss man wieder zudecken, kann aber
im Fall Typ 3 im nächsten Zug sofort ein Paar aufdecken oder, im Fall Typ 4, weiß man zumindest
zwei neue Karten unter den Zugedeckten (B ist im nächsten Zug um 2 größer).
- Mehr kann man im Memory offenbar nicht tun, um seine Chancen zu erhöhen. Wie man leicht
erkennt, ist die ungünstigste Situation, zu Anfang zwei verschiedene Karten zu erwischen und
dann immer im Schritt A eine neue und im Schritt B eine bekannte Karte, aus den vorigen Zügen zu
ziehen, da man dann jeweils einen Fehler pro Schritt macht, aber im Gegensatz zu zwei neuen Karten,
nur eine neue Karte kennenlernt. In diesem Fall beendet man das Spiel mit 7 Fehlern.
(Würde man
immer "falsche Karten" erwischen, hätte man nach vier Zügen zwar 4 Fehler, weiß dann aber 8
verschiedene Karten und kann dann ohne weiteren Fehler auf jeden Fall fertigmachen!)
- Die günstigste Situation ist unabhängig von der Sielweise des Spielers natürlich,
8 mal auf Anhieb Paare zu erwischen und damit mit 0 Fehlern zu spielen.
Erläuterungen zum Rechenverfahren
(zurück)Man kann nun alle möglichen Spielverläufe in Form eines sog. Baumdiagramms aufzeichnen, wobei das Baumdiagramm höchstens 7 Ebenen besitzt (da ein optimal gespieltes Spiel maximal Länge 7 hat) und sich an jedem Knoten vier mal verzweigt. Die vier Fälle die bei jedem Zug in einem optimal gespielten Spiel auftreten können, sind dem Teil " Was ist eine optimale Gewinnstrategie?" zu entnehmen. Etwas zusammengefasst sind es die Fälle:
- Fall: Die erste neu aufgedeckte Karte gehört zu den B bekannten Karten,
Spielerreaktion: dann wird man als zweite Karte natürlich sofort die Partnerkarte zur ersten aufdecken.
Auswirkung des Falls: B und U verringern sich auf diesen Zug hin jeweils um 1, kein Fehler muß hingenommen werden!
Wahrscheinlichkeit des Falls: B / U
-
Fall: Die erste neu aufgedeckte Karte gehört nicht zu den B bekannten Karten, die zweite ist wieder eine neue Karte,
Spielerreaktion: Die zwei Karten werden einfach wieder umgedreht.
Auswirkung des Falls: B erhöht sich um 2, U verringert sich um 2 und ein Fehler wird hingenommen.
Wahrscheinlichkeit des Falls: (U - B) / U * (U - B - 2) / (U - 1)
-
Fall: Die erste neu aufgedeckte Karte gehört nicht zu den B bekannten Karten, die zweite ist eine vor dem Zug bekannte Karte.
Spielerreaktion: Man muß beide Karten wieder zudecken, weiß aber ein zusammengehöriges Kartenpaar, dass man auch sogleich in einem Folgezug aufdeckt.
Auswirkung des Falls: B bleibt daraufhin gleich, U verringert sich um 2 und der Fehler des ersten Zuges muss hingenommen werden.
Wahrscheinlichkeit des Falls: (U - B) / U * B / (U - 1)
-
Fall: Die erste neu aufgedeckte Karte gehört nicht zu den B bekannten Karten, die zweite ist aber zur eben umgedrehten passend.
Spielerreaktion: Keine besondere Reaktion, sozusagen Idealfall durch Glück.
Auswirkung des Falls: U verringert sich um 2, der Rest bleibt unverändert (B und Fehlerstand).
Wahrscheinlichkeit des Falls: (U - B) / U * / (U - 1)
Es können nun durch Aneinanderreihung dieser Fälle alle Spielchroniken erzeugt werden, bis U=0 und
damit auch B=0 ist. Die Spielsituationen werden durch die Stände (B; U; Fehler)
charakterisiert. Jede Spielchronik mündet in eine Spielsituation (0; 0; Fehler) und hat
eine zu bestimmende Wahrscheinlichkeit.
Gemeinsame Startsituation ist (0; 16; 0). Zuerst werden mittels induktiven EXCEL-Funktionen
alle Spielchroniken mit Endfehlerstand und Wahrscheinlichkeit berechnet. Zuletzt werden die
Wahrscheinlichkeiten alle Spielchroniken mit gleichem Endfehlerstand addiert und darauf der
Erwartungswert des Endfehlerstandes berechnet.
Zwei Schlusssituationen werden getrennt behandelt, um Rechnerleistung zu sparen
(sie können bei optimaler Spielweise auf jeden Fall zu Ende gespielt werden,
ohne neue Fehler zu erzeugen).
- (5 Fall:) Es gibt zuletzt nur noch zwei Karten, die noch nie aufgedeckt waren.
- (6 Fall:) Noch nie aufgedeckte und bereits aufgedeckte Karten sind gleich viele vorhanden.
Die Tabellen 0 - 7 wurden rekursiv erstellt, aber immer wieder von Hand sortiert,
von Fällen mit Wahrscheinlichkeit=0 gereinigt, ... , um Rechnerleistung zu sparen.
Würde man alle Chroniken mit bis zu 7 Zügen aufschreiben,
wären dies zwar etwa 16.000 Züge, was in EXCEL mit etwas über 60.000 Zeilen zwar prinzipiell
berechenbar sein müsste. Dieser Ansatz führte trotz immer wieder variierter Versuche jedoch
stets zu Rechnerabstürtzen. Viele der Spielchroniken haben aber
Zwischenstände mit Wahrscheinlichkeit=0, die man eliminieren kann,
bevor sie sich weiter verzweigen. Auch kann man Chroniken mit gleichen Endsituationen,
auf die man gemäß Fall 5 und 6 reagieren kann, zusammenfassen.
Tabelle mit allen möglichen Spielverläufen und deren Wahrscheinlichkeiten
(zurück)
Nachstehende Tabelle wurde mit dem Microsoft Excel Internet-Assistenten erstellt.
| Häufigkeit von Fehlern bei 4 x 4 - Memorys | |
| (unterstellt wird eine optimale Spielstrategie) | |
| Mögliche Fehler | Häufigkeit |
| 0 Fehler (Details 2KB) | 0,00005% |
| 1 Fehler (Details 58KB) | 0,00829% |
| 2 Fehler (Details 588KB) | 0,45170% |
| 3 Fehler (Details 1,8MB) | 8,65130% |
| 4 Fehler (Details 2,1MB) | 45,90866% |
| 5 Fehler (Details 0,9MB) | 41,09431% |
| 6 Fehler (Details 154KB) | 3,87316% |
| 7 Fehler (Details 7KB) | 0,01253% |
| Mittlere Fehlerhäufigkeit | 4,4 |
Alle möglichen Spielchroniken sind tabelliert, nach verursachten Fehlern geordnet und mit ihrer Wahrscheinlichkeit versehen. Klicken Sie auf den entsprechenden Link um die Einzelergebnisse einzusehen! Die Zahlen in den Chroniken beziehen sich auf die obige Numerierung der vier möglichen Fälle (+ Sonderfälle 5 und 6).
Grafik
(zurück)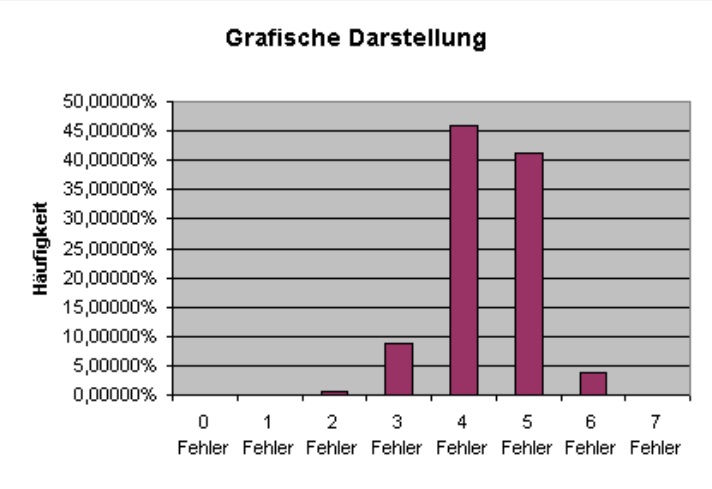
Letzte Aktualisierung 12.01.01